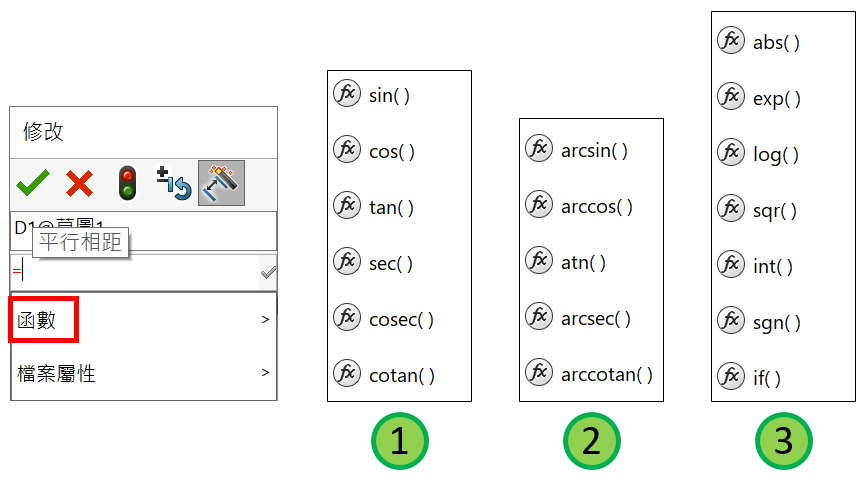
SolidWorks 數學關係式支援 18 個函數,在尺寸修正視窗輸入等於 ( = ) 可見到函數清單,由於清單太長不容易顯示,所以拆開為 3 部分解釋,由上到下分為 : 1. 三角函數、2.反三角函數、3.常用函數,以及在最後一節補充隱藏版函數,雖在清單沒有顯示,但可以輸入函數名稱方式使用函數功能。
內容目錄
1. 三角函數
說明三角函數(Trigonometric functions)的 6 種函數 : 1.sin(正弦)、2.cos(餘弦)、3.tan(正切)、4.cot(餘切)、5.sec(正割)、6.csc(餘割)。
1-1. sin 函數
正弦 ( Sine,縮寫sin ),是週期函數。最小正週期為 2π ,值域是【-1,1】,定義域是整個實數集。
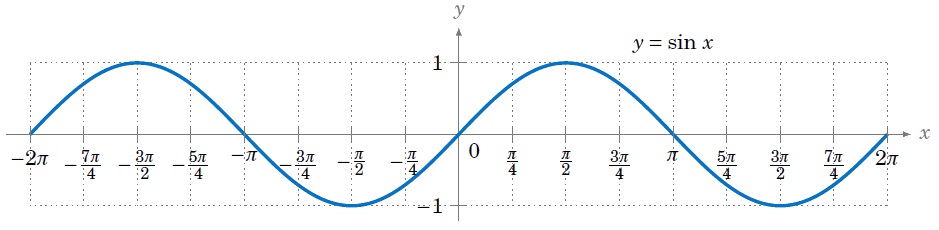
A. 使用說明及範例
於函數括號內輸入週期角度,角度須由 π 換算為實際角度。

A : sin ( 0 ) = 0
B : sin ( π/2 ) = sin ( 90 ) = 1
C : sin ( π ) = sin ( 180 ) = 0
D : sin ( 3π/4 ) = sin ( 270 ) = -1
E : sin ( 2π ) = sin ( 360 ) = 0
1-2. cos 函數
餘弦 ( Cosine,縮寫cos ),是週期函數。最小正週期為 2π ,值域是【-1,1】,定義域是整個實數集。
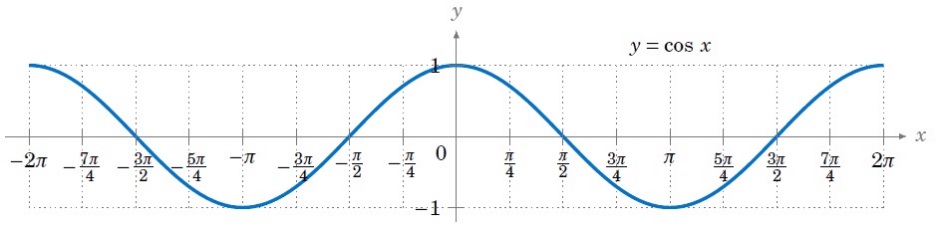
A. 使用說明及範例
於函數括號內輸入週期角度,角度須由 π 換算為實際角度。
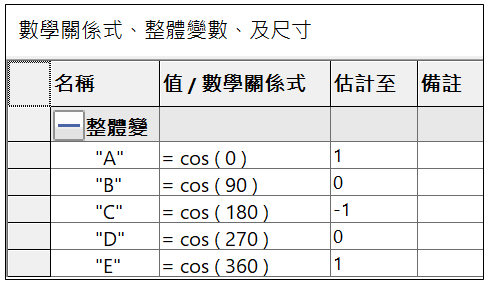
A : cos ( 0 ) = 1
B : cos ( π/2 ) = cos ( 90 ) = 0
C : cos ( π ) = cos ( 180 ) = -1
D : cos ( 3π/4 ) = cos ( 270 ) = 0
E : cos ( 2π ) = sin ( 360 ) = 1
1-3. tan 函數
正切 ( Tangent,縮寫tan ),是週期函數。最小正周期為 π,值域是整個實數集,定義域落在{x|x≠kπ+(π/2),k∈Z}。
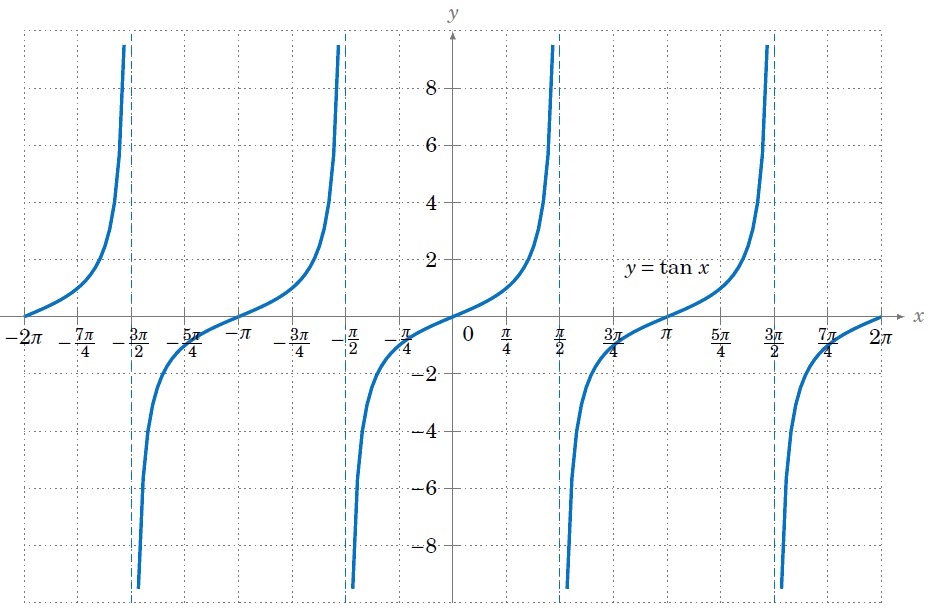
A. 使用說明及範例
於函數括號內輸入週期角度,角度須由 π 換算為實際角度。

A : tan ( 0 ) = 0
B : tan ( π/4 ) = tan ( 45 ) = 1
C : tan ( 3π/4 ) = tan ( 135 ) = -1
D : tan ( π ) = tan ( 180 ) = 0
E : tan ( 5π/4 ) = tan ( 225 ) = 1
1-4. sec 函數
正割 ( Secant,縮寫sec ),是週期函數。最小正周期為 2π,值域是絕對值大於等於一的實數,定義域不是整個實數集。
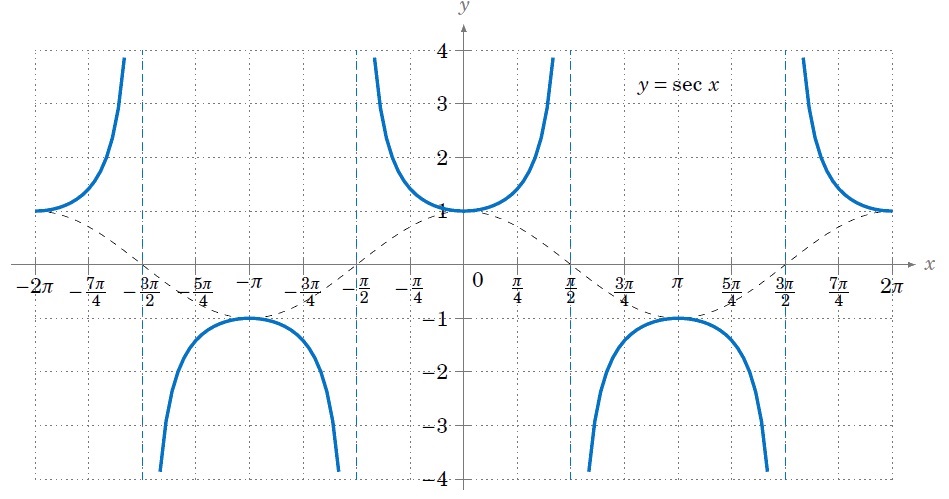
A. 使用說明及範例
於函數括號內輸入週期角度,角度須由 π 換算為實際角度。

A : sec ( 0 ) = 1
B : sec ( π/4 ) = sec ( 45 ) = 1.41421
C : sec ( 3π/4 ) = sec ( 135 ) = -1.41421
D : sec ( π ) = sec ( 180 ) = -1
E : sec ( 5π/4 ) = sec ( 225 ) = -1.41421
1-5. cosec 函數
餘割 ( Cosecant,縮寫csc ),是週期函數。最小正周期為 2π,值域是絕對值大於等於一的實數,定義域不是整個實數集。
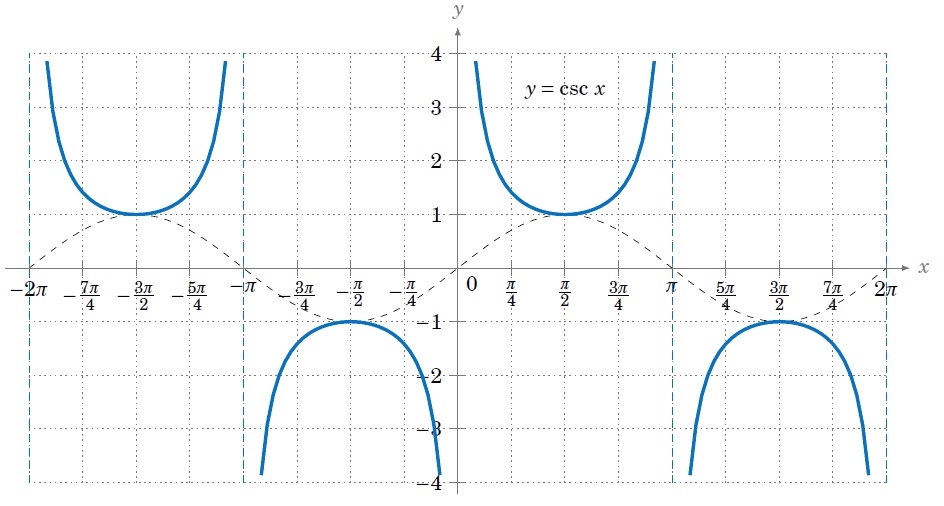
A. 使用說明及範例
於函數括號內輸入週期角度,角度須由 π 換算為實際角度。
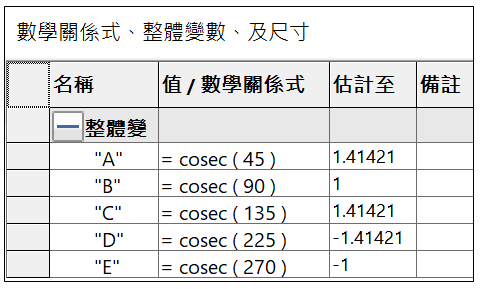
A : cosec ( π/4 ) = cosec ( 45 ) = 1.41421
B : cosec ( π/2 ) = cosec ( 90 ) = 1
C : cosec ( 3π/4 ) = cosec ( 135 ) = 1.41421
D : cosec ( 5π/4 ) = cosec ( 225 ) = -1.41421
E : cosec ( 3π/2 ) = cosec ( 270 ) = -1
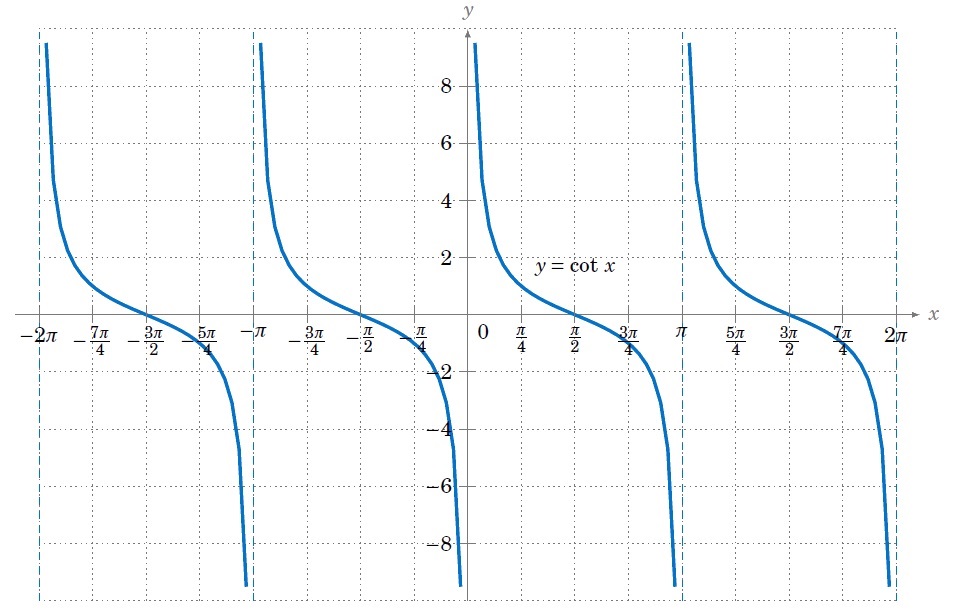
1-6. cotan 函數
餘切 ( Cotangent,縮寫cot ),是週期函數。最小正周期為 π,值域是整個實數集,定義域是整個不等於kπ的實數的集合,k為整數。
A. 使用說明及範例
於函數括號內輸入週期角度,角度須由 π 換算為實際角度。
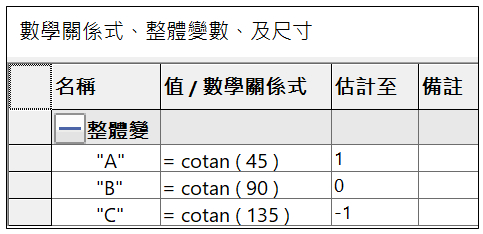
A : cotan ( π/4 ) = cotan ( 45 ) = 1
B : cotan ( π/2 ) = cotan ( 90 ) = 0
C : cotan ( 3π/4 ) = cotan ( 135 ) = -1
2. 反三角函數
說明反三角函數(Inverse trigonometric function)的 5 種函數 : 1. arcsin(反正弦)、2. arccos(反餘弦)、3. atn(反正切)、4. arcsec(反正割)、5. arccotan(反餘切),不支援arccsc(反餘割)。
2-1. arcsin 函數
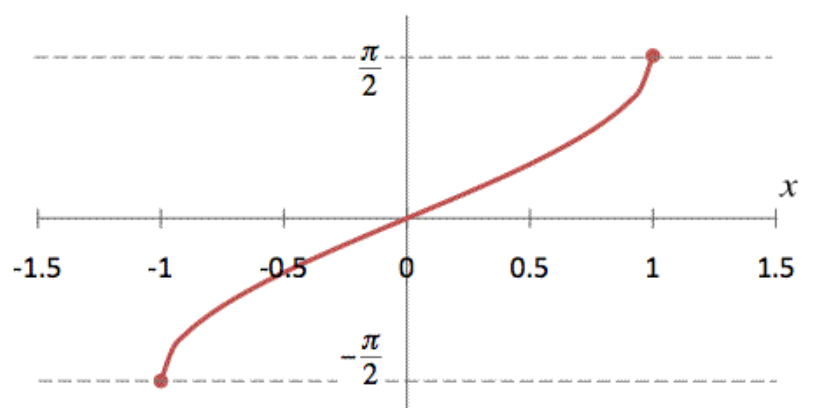
反正弦 ( Arcsine,縮寫arcsin ),是正弦反函數,值域是【-π/2,π/2】,定義域是【-1,1】。在原始定義,若輸入值不在區間【-1,1】,是沒有意義,但是三角函數擴充到複數之後,若輸入值不在區間【-1,1】,將傳回複數。
A. 使用說明及範例
於函數括號內輸入定義域【-1,1】間的值。

A : arcsin ( -1 ) = 90
B : arcsin ( 0 ) = 0
C : arcsin ( 1 ) = 90
2-2. arccos 函數
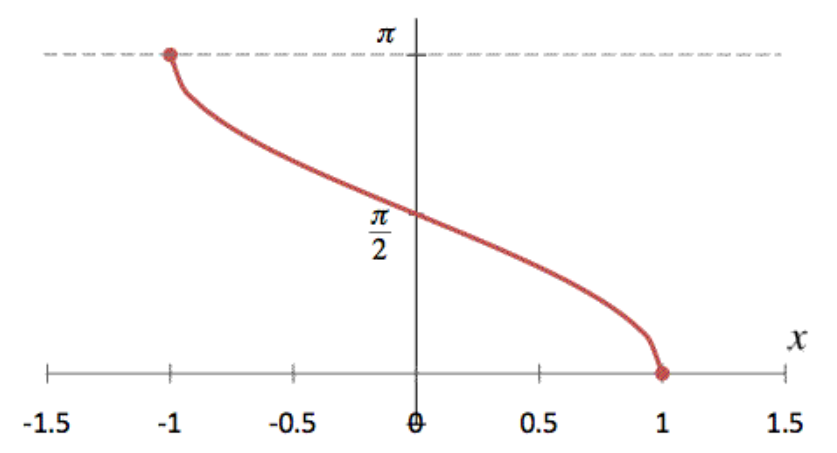
反餘弦 ( Arccosine,縮寫arccos ),為餘弦反函數,值域是【0,π】,定義域是【-1,1】。在原始定義,若輸入值不在區間【-1,1】,是沒有意義,但是三角函數擴充到複數之後,若輸入值不在區間【-1,1】,將傳回複數。
A. 使用說明及範例
於函數括號內輸入定義域【-1,1】間的值。
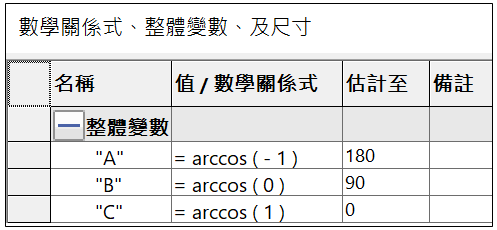
A : arccos ( -1 ) = 180
B : arccos ( 0 ) = 90
C : arccos ( 1 ) = 0
2-3. atn 函數
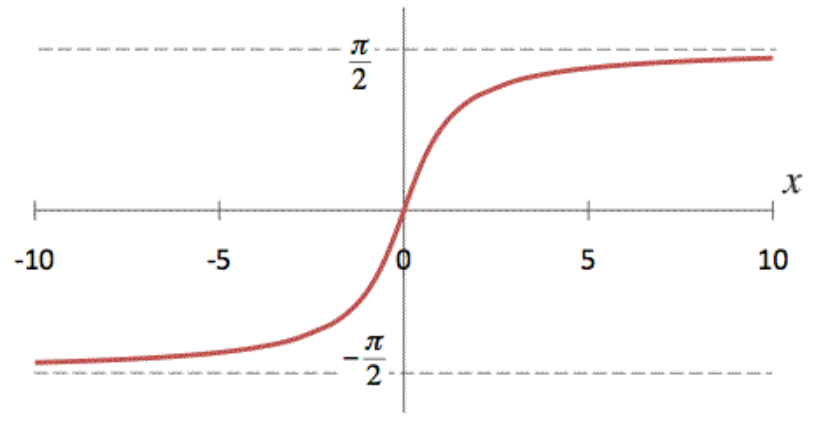
反正切 ( Arctangent,縮寫arctan、arctg ),為正切反函數,值域是【-π/2,π/2】,定義域是全體實數。
A. 使用說明及範例
於函數括號內輸入定義域 : 全體實數值。配合上表輸入 X 軸數值,可對應出 Y軸 之答案。

A : atn ( -10 ) = -84.2894
B : atn ( -5 ) = -78.6901
C : atn ( 0 ) = 0
D : atn ( 5 ) = 78.6901
E : atn ( 10 ) = 84.2894
2-4. arcsec 函數
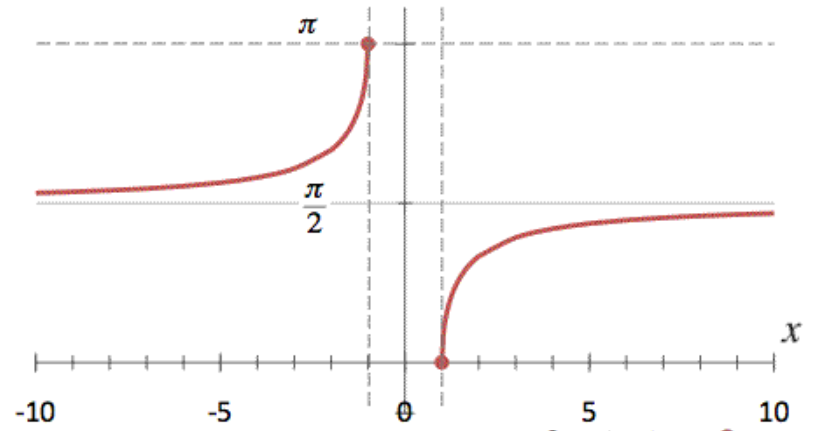
反正割 (Arcsecant,縮寫arcsec ),為正割反函數,值域是【0,π/2) U (π/2,0】,定義域是(-∞,-1] U [1,+∞)。
A. 使用說明及範例
於函數括號內輸入定義域 : (-∞,-1] U [1,+∞)。配合上表輸入 X 軸數值,可對應出 Y軸 之答案。

A : arcsec ( -10 ) = 95.7392
B : arcsec ( -5 ) = 101.537
C : arcsec ( -1 ) = 180
D : arcsec ( 1 ) = 0
E : arcsec ( 5 ) = 78.463
F : arcsec ( 10 ) = 84.2608
2-5. arccotan 函數
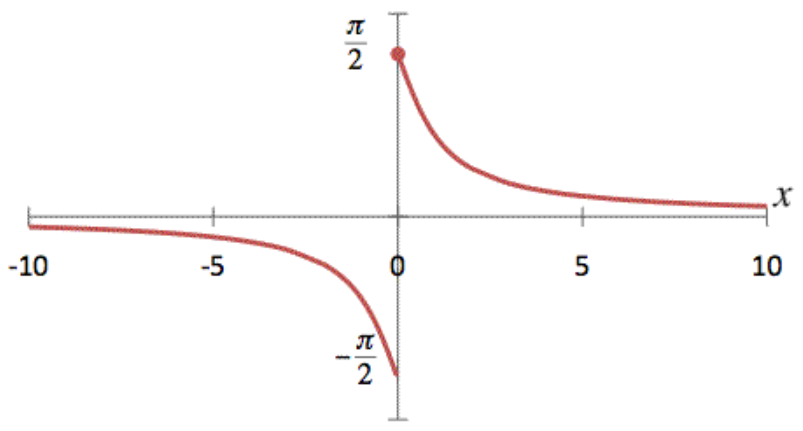
反餘切 ( Arccotangent,縮寫arccot ),為餘切反函數,值域是【0,π】,定義域是全體實數。
A. 使用說明及範例
於函數括號內輸入定義域 : 全體實數。配合上表輸入 X 軸數值,可對應出 Y軸 之答案。
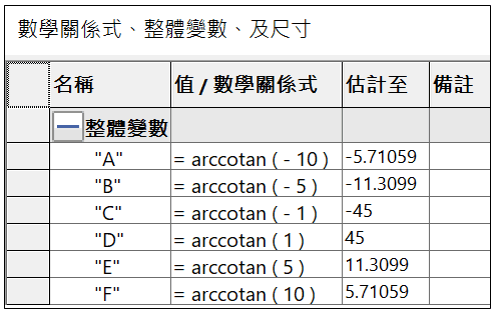
A : arccotan ( -10 ) = -5.71059
B : arccotan ( -5 ) = -11.3099
C : arccotan ( -1 ) = -45
D : arccotan ( 1 ) = 45
E : arccotan ( 5 ) = 11.3099
F : arccotan ( 10 ) = 5.71059
3. 常用函數
說明 7 種常用函數 : 1. abs ( 絕對值 )、2. exp ( 指數 )、3. sqr ( 平方根 )、4. int ( 無條件捨去 ) 、5. sgn ( 邏輯 ) 、6. if ( 判斷 )。
3-1. abs 函數
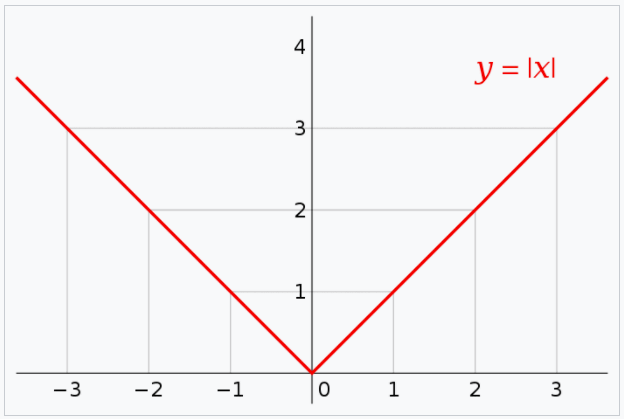
絕對值 ( Absoulte ),以前 3 個字母作為函數名稱縮寫 Abs,絕對值是永遠大於或等於 0 的實數。
A. 使用說明及範例
在 Abs 函數括號內輸入任意正負數值,經關係式計算後,答案永遠為正數。

A : abs ( 2 ) = 2
B : abs ( 0 ) = 0
C : abs ( -2 ) = 2
D : abs ( -50 ) = 50
3-2. exp 函數
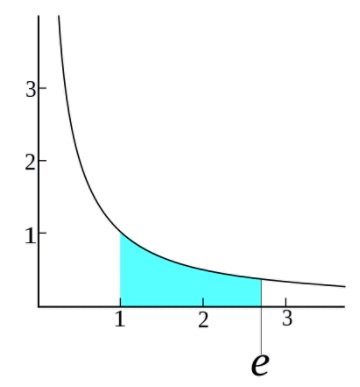
指數(exponential),又稱自然常數、自然底數,或尤拉數(Euler’s number),以瑞士數學家尤拉命名。SolidWorks 取前 3 字母 exp 為函數縮寫,數學以 e 表示,常數 e 等於 2.71828182845904。
A. 使用說明及範例
在指數函數括號內輸入常數 e 的乘冪次數,例如 : exp(2)答案為 e²=7.3890561,exp(3)答案為 e³=20.0855…以此類推。
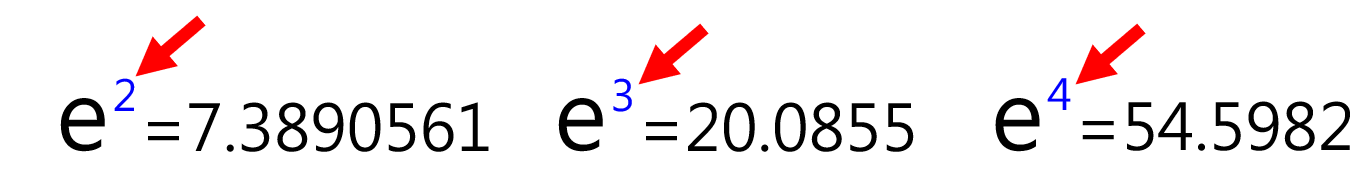
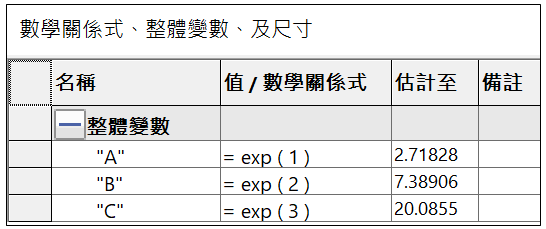
A : exp ( 1 ) = 2.71828
B : exp ( 2 ) = 7.38906
C : exp ( 3 ) = 20.0855
3-3. sqr 函數
平方根函數 ( Square Root Function ),以 2 個單字前的字母作為函數縮寫。
A. 使用說明及範例
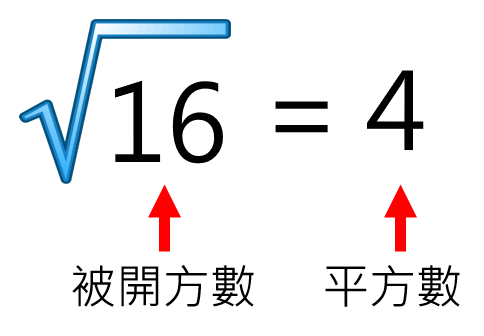
在平方根函數括號內輸入被開方數,經關係式計算後答案為平方數。

A : sqr ( 4 ) = 2
B : sqr ( 9 ) = 3
C : sqr ( 16 ) = 4
D : sqr ( 25 ) = 5
參考資料 : Sqr 函數
3-4. int 函數
無條件捨去所有小數位數,使數值保持為整數。
A. 使用說明及範例
於函數括號內輸入任意正負數值,經關係式計算後答案為整數。
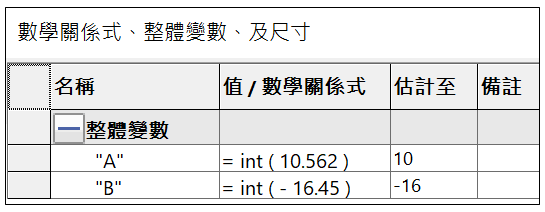
A : int ( 10.562 ) = 10
B : int ( -16.45 ) = -16
3-5. sgn 函數
符號函數(Sign function),以 sgn 作為函數名稱縮寫,是邏輯函數。為避免英文讀音與正弦函數(sine)搞混,也稱為Signum。用來決定數字的正負號,若為正數傳回 1、為 0 傳回零(0)、為負數則傳回 -1。
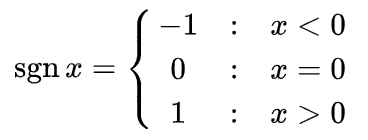
A. 使用說明及範例
在符號函數括號內輸入任意正負數值,經關係式計算後答案僅有3種定義數值 : 1、0、-1。
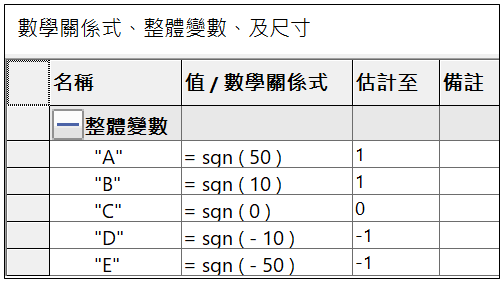
A : sgn ( 50 ) = 1
B : sgn ( 10 ) = 1
C : sgn ( 0 ) = 0
D : sgn ( -10 ) = -1
E : sgn ( -50 ) = -1
3-6. if 函數
是 Visual Basic ( VB ) 函數,用來設定判斷條件,指定當數值符合或不符合所回傳的個別訊息。
A. 使用說明及範例
在 IIF函數 括號內依序輸入 : 判斷條件、條件成立傳回值、條件不成立傳回值,在 3 個數字間加入逗號 ( , ) 區別。
公式 = IIF ( 判斷條件 , 條件成立傳回值 , 條件不成立傳回值 ),計算式 = IIF ( “A “>= 100 , 1 , 0 ),說明 : 如果 A = 150,符合公式 >100,所以 B = 1;若 A = 70,不符合公式 >100,所以 B = 0。
對於 IF 判斷式更詳細的說明,會以另外一篇文章繼續說明。

4. 補充函數
4-1. Round 函數
Round 函數將小數四捨五入進位至設定的小數位數,此函數清單沒有支援,必須自行輸入函數名稱,屬於隱藏版指令。但 SolidWorks 函數功能不足 Excel 函數,不支援 Roundup ( 無條件進位 )、Rounddown ( 無條件捨去 ),或實數進位功能。
A. 使用說明及範例
在 Round函數括號內輸入數值及保留的小數位數,在 2 個數字間加入逗號 ( , ) 區別。
公式 = round ( 數值 , 保留小數位數 ),計算式 = round ( 2.149 , 1 ),說明 : 2.149 取小數後 1 位,由於小數第 2 位為 4 捨去不進位,計算結果為 2.1。
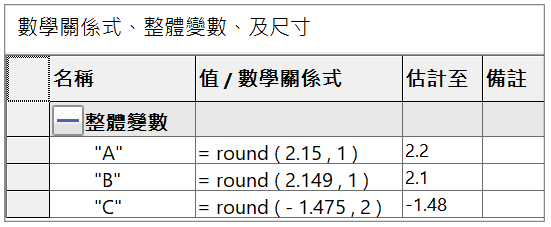
A : round ( 2.15 , 1 ) = 2.2
B : round ( 2.149 , 1 ) = 2.1
C : round ( -1.475 , 2 ) = -1.48






